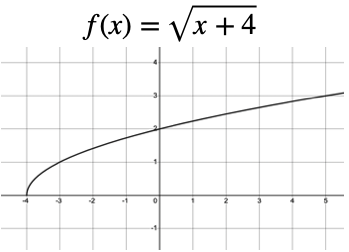
Download this Domain and Range worksheet with 10 questions and answers as a practice test.
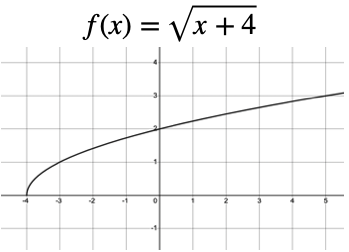
The domain of a function is the complete set of possible values of the independent variable.
In plain English, this definition means:
The domain is the set of all possible x-values which will make the function "work", and will output real y-values.
When finding the domain, remember:
This tool combines the power of mathematical computation engine that excels at solving mathematical formulas with the power of GPT large language models to parse and generate natural language. This creates math problem solver thats more accurate than ChatGPT, more flexible than a calculator, and faster answers than a human tutor.
After finishing this lesson head over to our interactive calculator to help you find the Domain and Range of a Fuction.
Here is the graph of `y = sqrt(x+4)`:
Need a graphing calculator? Read our review here:
The domain of this function is `x ≥ −4`, since x cannot be less than ` −4`. To see why, try out some numbers less than `−4` (like ` −5` or ` −10`) and some more than `−4` (like ` −2` or `8`) in your calculator. The only ones that "work" and give us an answer are the ones greater than or equal to ` −4`. This will make the number under the square root positive.
Notes:
In general, we determine the domain of each function by looking for those values of the independent variable (usually x) which we are allowed to use. (Usually we have to avoid 0 on the bottom of a fraction, or negative values under the square root sign).
The range of a function is the complete set of all possible resulting values of the dependent variable (y, usually), after we have substituted the domain.
In plain English, the definition means:
The range is the resulting y-values we get after substituting all the possible x-values.
Let's return to the example above, `y = sqrt(x + 4)`.
We notice the curve is either on or above the horizontal axis. No matter what value of x we try, we will always get a zero or positive value of y. We say the range in this case is y ≥ 0.
The curve goes on forever vertically, beyond what is shown on the graph, so the range is all non-negative values of `y`.
The graph of the curve y = sin x shows the range to be betweeen −1 and 1.
The domain of y = sin x is "all values of x", since there are no restrictions on the values for x. (Put any number into the "sin" function in your calculator. Any number should work, and will give you a final answer between −1 and 1.)
From the calculator experiment, and from observing the curve, we can see the range is y betweeen −1 and 1 . We could write this as −1 ≤ y ≤ 1.
Where did this graph come from? We learn about sin and cos graphs later in Graphs of sin x and cos x
Note 1: Because we are assuming that only real numbers are to be used for the x-values, numbers that lead to division by zero or to imaginary numbers (which arise from finding the square root of a negative number) are not included. The Complex Numbers chapter explains more about imaginary numbers, but we do not include such numbers in this chapter.
Note 2: When doing square root examples, many people ask, "Don't we get 2 answers, one positive and one negative when we find a square root?" A square root has at most one value, not two. See this discussion: Square Root 16 - how many answers?
Note 3: We are talking about the domain and range of functions, which have at most one y-value for each x-value, not relations (which can have more than one.).
It's always a lot easier to work out the domain and range when reading it off the graph (but we must make sure we zoom in and out of the graph to make sure we see everything we need to see). However, we don't always have access to graphing software, and sketching a graph usually requires knowing about discontinuities and so on first anyway.
As meantioned earlier, the key things to check for are:
Find the domain and range of the function `f(x)=sqrt(x+2)/(x^2-9),` without using a graph.
In the numerator (top) of this fraction, we have a square root. To make sure the values under the square root are non-negative, we can only choose `x`-values grater than or equal to -2.
The denominator (bottom) has `x^2-9`, which we recognise we can write as `(x+3)(x-3)`. So our values for `x` cannot include `-3` (from the first bracket) or `3` (from the second).
We don't need to worry about the `-3` anyway, because we dcided in the first step that `x >= -2`.
So the domain for this case is `x >= -2, x != 3`, which we can write as `[-2,3)uu(3,oo)`.
To work out the range, we consider top and bottom of the fraction separately.
Numerator: If `x=-2`, the top has value `sqrt(2+2)=sqrt(0)=0`. As `x` increases value from `-2`, the top will also increase (out to infinity in both cases).
Denominator: We break this up into four portions:
When `x=-2`, the bottom is `(-2)^2-9=4-9=-5`. We have `f(-2) = 0/(-5) = 0.`
Between `x=-2` and `x=3`, `(x^2-9)` gets closer to `0`, so `f(x)` will go to `-oo` as it gets near `x=3`.
For `x>3`, when `x` is just bigger than `3`, the value of the bottom is just over `0`, so `f(x)` will be a very large positive number.
For very large `x`, the top is large, but the bottom will be much larger, so overall, the function value will be very small.
So we can conclude the range is `(-oo,0]uu(oo,0)`.
Have a look at the graph (which we draw anyway to check we are on the right track):
We can see in the following graph that indeed, the domain is `[-2,3)uu(3,oo)` (which includes `-2`, but not `3`), and the range is "all values of `f(x)` except `F(x)=0`."